分度圆直径d等于模数m乘以齿数z,即m=d/z。
模数的理解
它直接关联着齿距,从而反映了齿轮齿厚的大小,是齿轮齿本身尺寸的重要指标。
在齿轮的众多参数中,模数m是一个衍生参数。图1展示了其推导过程。
首先,我们定义了齿距p,并通过公式πd=pZ推导出d=p/πZ。在此基础上,我们人为地设定模数m等于p/π,以此作为齿轮设计的基础参数。
下图说明了定义一个齿轮的有关概念
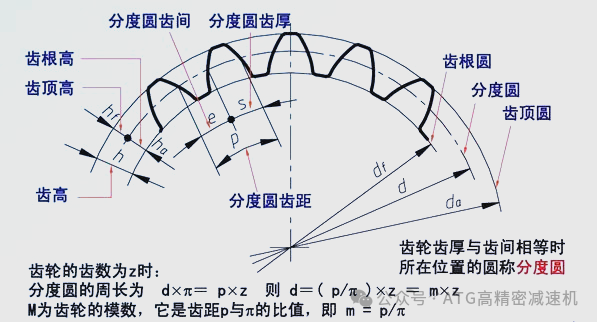
分度圆:标准齿轮中为槽宽和齿厚相等的那个圆,即e=s。
齿轮并非孤立的,它们往往成对出现,形成传动比。这引发了一个核心问题:如何确保两个尺寸不同的齿轮能够顺畅啮合?
显然,要实现这一点,它们的模数和压力角必须分别相等。然而,从齿轮的发明者的视角来看,事情并非总是那么直观。最初,人们可能仅仅使用矩形齿,而没有渐开线的概念。
为了确保两个齿轮能够顺利啮合,一个齿轮的齿厚必须与另一个齿轮的齿槽宽度相等。否则,它们可能会卡住。因此,需要找到一个能够直接反映齿轮齿厚的物理量。
最终,聪明的先辈们发现了齿距这个量。只要齿距相等,无论齿轮的齿数如何,它们都能顺畅地啮合。这一发现至关重要。
一旦确定了齿距,我们可以通过将齿数与齿距相乘来得到周长。进而,我们可以推导出模数的定义:模数实际上代表了齿距,即齿的大小。这就是模数的物理意义。
分度圆是为了便于齿轮设计和制造而选择的一个尺寸参考。齿轮分度圆上具有标准的模数和标准的压力角。
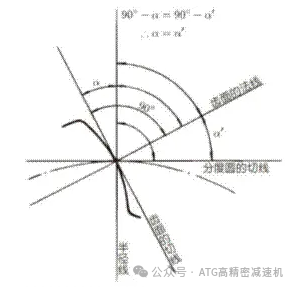
压力角:齿廓接触点的法线与分度圆切线之间的夹角α’。
压力角的大小对齿轮性能有着显著影响。压力角越小,齿轮的重合度越高,从而降低噪音,但这也可能导致更多的磨损和效率损失。另一方面,压力角越大,齿轮的啮合线越短,这有助于提高接触应力和齿根强度,但也可能对轴承提出更高要求,并可能增加摩擦和噪音。在实际应用中,常见的压力角值包括15°、17.5°、20°和25°。例如,20°压力角的齿轮常用于轻载和高速度传动场景,而25°压力角的齿轮则更适用于重载应用。
仟德亿传动科技(苏州)有限公司是集研发·制造销售·服务于一体的国家高新技术企业。公司立足于智能化、自动化装备核心零部件设计和制造,为客户提供智能驱动解决方案。积极开拓国内外市场,足迹遍布全球30余国。我们产品主要包括ATG高精密行星减速机、RV关节减速机、谐波减速机,中空旋转平台,换向器,转角器,分割器等传动机械产品。

